正态分布

正态分布是一个连续型的概率分布，其图形呈钟形曲线。它以其对称性和集中度特点而闻名，被广泛应用于统计学、自然科学、工程学和经济学等领域。正态分布的形状由两个参数决定，即均值（μ）和标准差（σ）。

定义

正态分布的定义可以通过其概率密度函数来描述。对于给定的随机变量X，其服从正态分布的概率密度函数如下：

P(x) = 1 / [(2π)^(1/2) σ] e^[-(x-μ)^2 / 2σ^2]

其中，P(x)表示随机变量X取值为x的概率，e是自然对数的底数（约等于2.71828），π是圆周率。μ表示正态分布的均值，σ表示标准差。

性质

正态分布具有以下几个重要的性质：

1.对称性：正态分布的概率密度函数关于均值对称，即在均值处取得最大值，并且两侧的曲线形状相同。

2.集中度：标准差σ越小，曲线越尖锐，分布越集中；标准差σ越大，曲线越平坦，分布越分散。

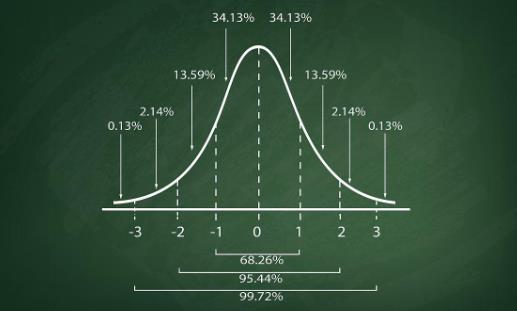
3.68-95-99.7规则：在正态分布中，约有68%的数据落在均值±1个标准差之间，约有95%的数据落在均值±2个标准差之间，约有99.7%的数据落在均值±3个标准差之间。

4.中心极限定理：当独立随机变量的数量足够大时，它们的平均值将近似服从正态分布。这个定理对于统计学中许多推断方法的合理性提供了理论基础。

概率公式

正态分布求概率的公式如下：

P(x) = 1 / [(2π)^(1/2) σ] e^[-(x-μ)^2 / 2σ^2]

其中，P(x)表示随机变量X取值为x的概率，e是自然对数的底数（约等于2.71828），π是圆周率。μ表示正态分布的均值，σ表示标准差。

这个公式可以用来计算随机变量X在给定取值x处的概率。通过将x代入公式中，我们可以得到相应的概率值。