傅里叶变换

傅里叶变换是一种数学工具，用于将一个函数或信号从时域转换到频域。它是法国数学家约瑟夫·傅里叶在19世纪提出的，被广泛应用于信号处理、图像处理、通信系统等领域。

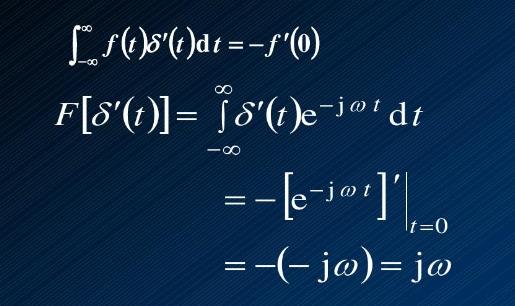
傅里叶变换的定义如下：对于一个连续函数f(t)，其傅里叶变换F(ω)定义为：

F(ω) = ∫[?∞, +∞] f(t) * e^(-iωt) dt

其中，F(ω)表示频域中的复数函数，ω表示频率，e为自然对数的底。傅里叶变换将函数f(t)分解成了不同频率的正弦和余弦波的叠加。

傅里叶变换具有许多重要性质，包括线性性、平移性、尺度性、共轭对称性和卷积定理等。这些性质使得傅里叶变换成为一种强大的工具，可以用来分析和处理各种类型的信号和数据。

傅里叶变换在许多领域中起着重要作用。首先，在信号处理中，通过将信号从时域转换到频域，我们可以分析信号的频谱特征，如频率成分、幅度和相位信息。这对于音频处理、图像处理和视频压缩等应用非常有用。

其次，在通信系统中，傅里叶变换被广泛应用于调制和解调过程中。通过将信号转换到频域，可以更好地理解信号在不同频率上的传输特性，从而优化通信系统的设计和性能。

此外，傅里叶变换还在图像处理中发挥着重要作用。通过将图像转换到频域，我们可以进行滤波、边缘检测和图像增强等操作，从而改善图像质量和提取有用的特征。