拉格朗日定理

拉格朗日定理，也被称为拉格朗日乘数法或约束条件法，是一种在最优化问题中常用的方法。它由意大利数学家约瑟夫·路易斯·拉格朗日于18世纪提出。该定理为求解带有约束条件的极值问题提供了一种有效的方法。

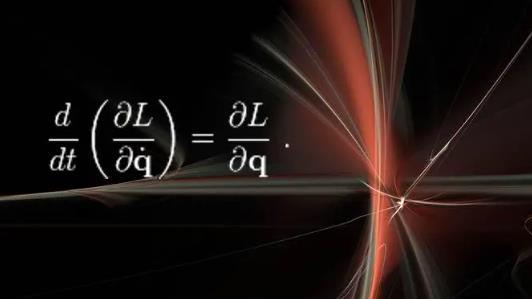
在数学中，一个极值问题通常可以表示为一个函数的最大值或最小值。然而，在现实生活中，很多情况下我们需要在满足一些限制条件下找到函数的极值。这就引入了约束条件。拉格朗日定理通过引入拉格朗日乘子来处理这类问题。

拉格朗日乘子法的基本思想是将约束条件与目标函数结合起来构建一个新的函数（称为拉格朗日函数）。通过对此函数求导并使其等于零，我们可以找到满足约束条件的极值点。

具体而言，假设我们要求解一个多元函数的最大值或最小值，并且存在一些约束条件。我们可以构建一个拉格朗日函数，该函数由目标函数与约束条件的乘积组成。然后，我们对这个函数进行求导，并令其等于零。通过求解这个方程组，我们可以找到满足约束条件的极值点。

拉格朗日定理的数学表达形式如下：

设 f(x) 是要优化的目标函数，g(x) 是约束条件，其中 x 是自变量向量。则拉格朗日函数 L(x, λ) 定义为：

L(x, λ) = f(x) - λ * g(x)

其中 λ 是拉格朗日乘子。

通过对 L(x, λ) 求导并令其等于零，我们可以得到一组方程。解这组方程即可得到满足约束条件的极值点。

拉格朗日定理在最优化问题中有广泛的应用。它不仅可以用于求解实际问题，还可以用于理论研究和证明最优性条件。此外，拉格朗日定理还与微积分、线性代数和凸优化等数学领域密切相关。